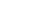Greatest Common Divisor (GCD) of 4, 18 and 33

The Greatest Common Divisor (GCD) of 4, 18 and 33 is the largest positive integer that equally divides all three numbers: 4, 18 and 33. Mathematically, the problem we are solving is:

GCD(4,18,33)

To solve the problem, we will list all the positive integers (divisors) that can be divided into 4, 18 and 33. We will then compare the lists of divisors to find the greatest divisor they have in common.

Divisors of 4:
1, 2, and 4.

Divisors of 18:
1, 2, 3, 6, 9, and 18.

Divisors of 33:
1, 3, 11, and 33.

When we compare the lists of divisors above, we see that the largest number they have in common is 1. Thus, the Greatest Common Divisor (GCD) of 4, 18 and 33 is:

GCD(4,18,33) = 1

Greatest Common Divisor Calculator
Please enter another two or three numbers below so we can calculate the Greatest Common Divisor (GCD) for you:

Greatest Common Divisor (GCD) of 4, 18 and 34
Go here for the next set of numbers that we calculated the Greatest Common Divisor for.